Warning: Invalid argument supplied for foreach() in /home/xs642990/dark-pla.net/public_html/wp-content/plugins/bravo-neo/bravo-neo.php(12) : eval()'d code on line 647
Pythonでオプションのグリークを計算してみよう、というお話です。
ポートフォリオ管理の都合上、いつかはやらないといけないな、とは思っていたのですが、急に取り組むことに…。
というのは、普段使っているInteractivebrokers(IB)で仕様変更があったのか、TWS上でもAPI経由でも、その日に値がついた銘柄でしか各グリーク値が取得できなくなってしまったのですね。
何言っているかわからないと思うので画像添付しますと、
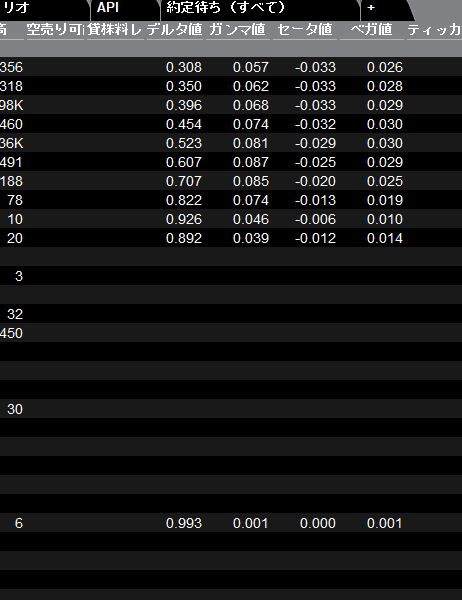
値がついた銘柄については多分その時点での各グリーク値が表示されているのですが、それ以外はまったくの空白。
それでも、例えばS&P500のオプションとかメジャーなものだったら問題ないでしょう。
各銘柄とも、絶えず値は付いていますから。
自分はVIXオプションとかを触っているので、そうすると気配値はあるものの取引は皆無、なんていうケースはざらにあるわけです。期先だと特に。
で、閑散マーケットだとかなりの虫食いですね…。
これの何が困るかというと、自分が保有している銘柄のグリーク値が取得できないと、ポートフォリオの状況がつかめないという点ですね。
まあ、今までが怠惰で自分で計算もせずに表示されたもの、もしくはAPI経由で取ってきた数字を検証もせずに足し上げてただけなんですけど。
いずれは手元で計算したもので管理しないとなー、なんて思っていたわけですが、こうやって突如として作業に追い込まれます…。
ま、そんなボヤキはともかく。
作業の方針は以下の通り。
1.TWSあるいはAPI経由で、虫食いでかまわないので必要なオプションのリストのボラティリティ(IV)を取得。
2.リストの各銘柄でIVを予想して穴埋め
3.PythonのQuantLibで各グリーク値を算出
1.IV取得
銘柄のIVを取得します。
TWSからCSVダウンロードでも、API経由での取得でも構いませんが、このあたりのデータの取り回しは本題ではないので今回は割愛。
IVも各グリーク値と同様に、値がつかない場合には欠損するようになってます。
2.IV欠損値を穴埋め
ボラティリティカーブの推計は、それはそれで一つのテーマです。
でも、今回は欠損値の埋めなので、さっさと前後見て穴埋めしておくれ、ということで「interpolate」を使ってIVの数値リストを作ります。
df_vixo_1 = df_vixo_orgn[['Sec_Type', 'Expire_Date', 'Strike_Price', 'IV']].copy().sort_values(by=['Sec_Type', 'Expire_Date', 'Strike_Price'],ascending=[True, False, False]) df_vixo_2 = df_vixo_1.interpolate()
現役の人に見られたら笑われるでしょうが…、まあ投資は自己責任ですし。
とりあえず今は、全銘柄のIVを作ることが大事。
値がついていないとは言え、気配値はあるのだからその仲値からIVを算出させるという作業をさせたほうが望ましいので、次回はそれに取り組みます。
ということで、これで一応必要な全銘柄のIVが完成します。
3.QuantLibで各グリーク値を算出。
原資産価格、期間、IV、金利が用意できたらあとはQuantLibに突っ込みます。
方々のサイトを参考にしながら関数を作成しました。
日本語での解説は数サイトしかヒットしませんでしたが、それでも誤りがあったりして…。
def black(op, rate):
global flavor
calendar = ql.UnitedStates()
bussiness_convention = ql.ModifiedFollowing
settlement_days = 0
day_count = ql.Actual365Fixed()
interest_rate = rate
calc_date = ql.Date(op.Price_Date.day, op.Price_Date.month, op.Price_Date.year)
yield_curve = ql.FlatForward(calc_date, interest_rate, day_count, ql.Compounded, ql.Continuous)
ql.Settings.instance().evaluationDate = calc_date
option_maturity_date = ql.Date(op.Expire_Date.day, op.Expire_Date.month, op.Expire_Date.year)
strike = op.Strike_Price
spot = op.Px_Ord_Act
volatility = op.IV
if op.Sec_Type == 'C':
flavor = ql.Option.Call
elif op.Sec_Type == 'P':
flavor = ql.Option.Put
strikepayoff = ql.PlainVanillaPayoff(flavor, strike)
discount = yield_curve.discount(option_maturity_date)
T = yield_curve.dayCounter().yearFraction(calc_date, option_maturity_date)
stddev = volatility*math.sqrt(T)
black = ql.BlackCalculator(strikepayoff, spot, stddev, discount)
return black.value(), black.delta(spot), black.gamma(spot), black.vega(T)/100., black.theta(spot, T), T
「金利の入力はパーセントで行う」という解説記事を見ましたが、ここは直数字のようです。
まあ、しばらくゼロに近かったから、100倍違ってもあまり結果に影響が出なかったのかもしれません。
でも今や10年債でも4%弱?
じゃあ、無理してオプションなんか使ってリスクを取らなくてもいい?
なんて一瞬思ったりもしますが、まあそんなことを考えてしまうこと自体、「デフレマインド」に侵されているのかも。
あと、出力ではデルタとガンマは違和感がありませんでしたが、ベガとセータは違和感ありまくり。
おそらくベガはパーセントで出力されているっぽい。
なので、関数の出力の段階で100で割っておきました。
問題はセータで、数字に心当たりがないのですね。
そもそも解説サイトで見たアウトプットからしておかしかったですからね。
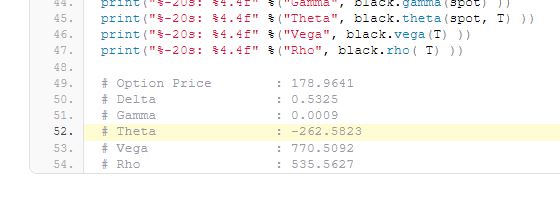
理論上のオプション価格が179ドルでセータが▲263ドル?
一日でオプション価格がマイナスになる?
これもパーセント表記なのか?、いやそれにしてもおかしい、とか、何に対する比率なんだ?、とか色々と考えてしまいますが、まあ、今回はここまで。
しばらく触りながら考えてみます。
ちなみに、作成した関数(black)の変数のうち、rateはそのものずばりの金利ですが、opはオプションの各銘柄の情報を持ったDataFrameです。
締め日、行使価格、CallPut種別、IVのデータを保有しています。
それにしてもInteractiveBrokers、仕様変更するなら前もって言って欲しい…。
でも、アメリカの会社ってこういうところありますよね。
自分はCBOEからも公表値を取得していますが、こういう半ばは公的な機関でもデータのフォーマットはときに突然に変わるので、難儀しますね。
日本ではあまりそういうことはないです。
こういうところも国民性でしょうか。